Hello, this is Joe Brusi
developer of 'PAcalculate', the free
multi-platform app for mobile phones and
tablets with calculators, reference
information such as pinouts, like this
useful speakON NL8 drawing, as well
as utilities such as an inclinometer, or
a flashlight, or a light screen for
theater applications. As far as
calculators go all of them include
relately lengthy help text here at the
bottom of the screen, or if we had a mobile
phone with a smaller screen, that text
screen would be accessed through an info
button like this. So that help
information is integrated within the app
but in this first video tutorial we
wanted to complete this information with
more detailed explanations on the sound
pressure level related calculators. The
SPL calculator calculates a resulting
total direct sound SPL. As well as doing
that it provides partial results that
you can see here on the right hand side
with the yellow background. On smaller
screens these corrections you'll find
them here at the bottom of the resulting
SPL. The calculation is for parameters
that you see on the screen:
sensitivity, power, number of speakers
with phase, and distance, so that means other
factors such as air attenuation,
reverberation, wind, or pressure gradients
that could curve the sound upwards are
not considered.
Also not considered is the loss of
sensitivity due to loudspeaker heating
or the signal crest factor, which means
that, depending on the amplifiers peak
power output, we will have more SPL for a
modern song with little dynamics than
for an uncompressed live sound audio or
songs from the 70s or 80s that were
recorded with much more dynamics than
those of today. The first input field is
sensitivity, which is the sound pressure
level produced referenced to a distance
of 1 meter with an input of 1 watt. Of
course, with sensitivity, the higher the
better because that means we have more
pressure for the same amount of input
power. Here we would enter the nominal
sensitivity from the manufacturer's spec
sheet but you should know that
sensitivities are not all born the same
and manufactures could use different
criteria that could result in slightly
different results, say plus minus 2 dB,
This sensitivity data that we introduced
here is the base SPL to which
corrections of power, number of speakers,
and distance are added, to get a total
resulting SPL. Next field is the power
that an amplified channel delivers to
each loudspeaker enclosure if we have a
box with more than one speaker then we
will treat it as a black box (because we
don't care what's inside) and we'll use
the number of boxes in the number of
loudspeakers field and in the
sensitivity field we'll use the
sensitivity of the entire box. If we have
several boxes connected to the same
amplifier channel then we'll enter the
power of the amplifier channel divided
by the number of
boxes. For example if we have 2 boxes
of 8 ohms each connected in parallel and
the amplifier delivers a power of a
thousand watts into a 4 ohm load then
we'll enter a power level of 500 watts.
It's important here to enter real power
based on RMS voltage. These days a lot of
manufacturers use peak power which is
twice as much or specifications based on
sinewave busrts, and that's a power
that cannot be maintained continuously.
Of course doubling the power means
adding 3 dB to the SPL so when we go
from 500 watts to 1000 watts we go
from 27 to 30 dB. Next is the number of
boxes that we enter the sensitivity for
in the first field of the calculator. As
we could expect doubling the number of
in-phase loudspeakers gets us an
increase of 6 dB in SPL, we double again
we have an extra 6 dB,if we double again to 8
we have a final total correction of 18
dB for 3 times doubling of the number of
speakers (from 1 to 2 to 4 and to 8)
whereas if we switch to the random phase
option, then it becomes 3 dB per doubling,
There a total of 9 dB for 8 speakers
carrying independent signals.
If we had 2 loudspeakers, one on each
side, carrying totally different signals,
such as instruments and voices that had
been panned completely to the right or to
the left, the sum of the sound pressure
level from each speaker would be 3 dB
more and that would happen pretty much
anywhere within a room. However if we
have the same two speakers carrying the
same signal, the only points in space
were the contributions from the two
speakers arrive at the same time is
this center line here, so only points
along this line would get a total
summation with no interference. therefore
6 dB extra decibels. However for any
other positions outside of this center
line the time arrivals from the sources
would be different and that would mean
the possibility of interference
Depending on the frequency and the time
arrival difference we might get total
summation, if we're lucky, 6 dB more.
Total cancellation if we are unlucky or
somewhere in between, that's why as a way
to make some kind of an average
throughout the area we tend to use the
random phase option in the SPL
calculator, so that we have an average
result which is also a conservative
result, so if there is any additional
gains because because of the spacings at
loudspeaker or the size of the room then
that's something that will will add to
our conservative estimate; we'd rather
have a more realistic conservative
estimate than overestimate the result.
On the other hand if we had an array of
subwoofers in the center, then pretty
much anywhere in the room time arrivals
are similar and considering that low
frequencies have very large wavelengths
In this case we could more or less use
the in-phase option for the SPL
calculation with relative certainty. As
the last field we have the change of SPL
contributed by distance to the source.
That works with the inverse square law,
so, of course, when we double the distance
(which we can enter in meters or feet) we
decrease 6 dB. If we double again we have
again 6 dB less; if we double again we
have a total of -18 dB. If we want
to calculate the effects of air
absorption for a specific frequency we
can use the air absorption calculator
here we can see the effect of different
variables in the total attenuation. For
instance, temperature does have an effect,
but if you watch the result field here
at the bottom it's not a great
difference. Let's go back to 25 degrees
(again we can use Celsius or Fahrenheit here)
As far as the relative, humidity water
is a much better conductor of sound than
air is, so that means the humidity has a
big impact: for instance here we have a
relative humidity of 15% with 3.5 dB
loss. If we go to 50% humidity
then that'll go down to 1,3.
Distance is also, of course, key. If we
change this 15 to, say, 100, that increases
dramatically. And frequency is also key:
if we change this 8,000 Hertz to 16,000
we would in this case almost quadruple
the air loss attenuation. The last sound
pressure level related calculator is SPL
addition, that allows us to add multiple
SPLs with a phase option that should be
used in the same way we saw before. Here
we can see for instance that if we have
two dB SPLs spaced by 10 dB, if the
phase option is at 'random phase' then the
end result is pretty much the largest
SPL we had to begin with, whereas if we
switch to 'in phase' now it's relatively
significant. As a final note, it's really
important to put the meaning of dB into
perspective and to remember what level
changes in dB mean: a change of 10 dB is
perceived as a change of doubling the
loudness, whereas 3 dB are basically
just a noticeable change and 1 dB
would hardly be noticeable at all,
especially when playing music. That's all
for now. See you next time!
For more infomation >> NGAKAK!! BULE BELAJAR "JONGLISH" (JAVANESE ENGLISH) - Duration: 5:09. 
For more infomation >> Hài Tết 2018 | Phim Hài Tết Tập 5 | Asia Entertainment - Duration: 28:46. 
For more infomation >> NAMHANHTRANG - NẤM LINH CHI: THẢO DƯỢC HỘ MỆNH CỦA NGƯỜI BỊ UNG THƯ - Duration: 2:04. 
For more infomation >> QUELLE PERCEPTION du TRAVAIL FAUT-IL AVOIR ? [ la civilisation du loisir #2 ] - Duration: 3:43. 
For more infomation >> Taken 2x03 Promo "Hammurabi" (SUB ITA) - Duration: 0:17. 
For more infomation >> 【 MMD x Yandere Simulator 】 ll Bii ll Vietsub CC】Look What You Made Me Do[Ayano Aishi] - Duration: 1:11. 
For more infomation >> PARCOURSUP : la solution miracle de l'ORIENTATION POST-BAC ? - Duration: 3:13. 
For more infomation >> Джеймс Хаббард "Первая Помощь Своими Руками" от Альпина Паблишер Рецензия Александры Рудамановой - Duration: 1:55. 
For more infomation >> Đêm Trong Khu Nhà Hoang .Thách Ai Dám Xem Hết Video Này .GHOST IN HOUSE .Thử Thách Săn Ma Lúc 12H - Duration: 10:50. 
For more infomation >> 結婚 仕事 感動話!仕事やめようかな。と妻に言うと返ってきたのは、まさかの返事だった! - Duration: 5:17. 
For more infomation >> Scribblenauts Showdown - Zwiastun ogłaszający - Duration: 0:31.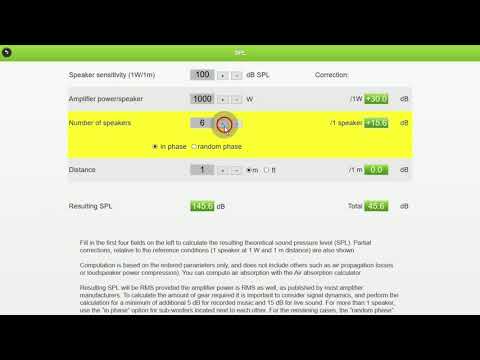 
Không có nhận xét nào:
Đăng nhận xét